
Voici la première partie de notre blogue Savoir Techno en deux volets sur l’équité algorithmique. Dans cette première partie, nous aborderons le sujet de l’équité algorithmique et analyserons les trois principales définitions qui définissent cette notion. Nous énumérerons les avantages et les inconvénients de chacune de ces définitions et décrirons les différents compromis qu’exigent celles-ci. Dans la deuxième partie, nous approfondirons notre analyse en examinant l’aspect pratique de l’équité algorithmique. Nous partons du principe que les lecteurs disposent de connaissances techniques de niveau opérationnel de l’intelligence artificielle (IA) et de l’apprentissage automatique (AA).
Présentation
L’équité est une notion fondamentale de l’éthique. La notion d’équité remonte au moins à l’époque de la Grèce antique. Des études philosophiques de cette époque fournissent des révélations importantes sur sa nature. La première est que l’équité, comme toutes les vertus, présente une ambiguïté particulière contrairement aux mathématiques ou aux sciences naturelles dont les lois sont pratiquement immuables (ou du moins visent à l’être). Les critères que nous utilisons pour déterminer si une ligne de conduite est équitable (ou inéquitable) sont variables et susceptibles de changer, surtout au fil du temps.
Cette variabilité s’explique par la nature même de la pensée éthique. Alors que les mathématiques et les sciences naturelles obtiennent leurs résultats par le calcul, l’équité est déterminée par délibération. La délibération est fondamentalement différente du calcul. Elle se distingue par son sens aigu de la temporalité. Lorsque nous délibérons, nous ne considérons pas simplement les faits d’un scénario par rapport aux réalités passées ou actuelles du monde, nous nous tournons également vers l’avenir, c’est-à-dire que nous pensons à nos aspirations.
Aristote (384 à 322 av. J.-C.), philosophe grec, avait une façon intéressante d’exprimer cette ambiguïté de l’équité tournée vers l’avenir. Selon lui, le comportement éthique humain se manifeste sous la forme d’une position moyenne entre deux extrêmesNote de bas de page 1. Aujourd’hui, ce point de vue est souvent exprimé en termes courants : nous jugeons qu’une chose est équitable (ou inéquitable) selon les circonstances.
Contrairement à l’équité, l’IA et l’AA (une des sous-disciplines de l’IA) sont des événements plus récents. Les termes « intelligence artificielle » (lien en anglais seulement) et « apprentissage automatique » (lien en anglais seulement) sont apparus dans les années 1950Note de bas de page 2. Malgré certaines périodes de financement réduit et de scepticisme, le domaine a beaucoup évolué, la recherche au 21e siècle s’avérant particulièrement productive. Durant cette période, les progrès réalisés dans le traitement informatique et les architectures de réseaux neuronaux ont conduit à la création d’une nouvelle sous-discipline : « l’apprentissage profondNote de bas de page 3 » (en anglais seulement).
L’IA et l’AA sont des technologies mathématiques modernes. Ils convertissent les tâches humaines en modèles statistiques complexes. L’IA et l’AA sont fondés sur « l’apprentissage par des exemples ». Généralement, l’IA et l’AA apprennent en optimisant les paramètres d’un modèle statistique selon les données d’apprentissage afin de réduire au minimum la valeur d’une fonction de coût.
L’IA/AA possèdent des caractéristiques opposées au concept éthique de l’équité. Au lieu d’un type d’ambiguïté productive, leur mode opérationnel utilise la précision des mathématiques. Pendant le perfectionnement, l’IA/AA utilisent les méthodes d’optimisation du calcul pour affiner la pente et la direction qui détermineront les paramètres de leur modèle. Pendant le déploiement, ils appliquent le modèle perfectionné à de nouveaux exemples pour calculer leurs résultats.
De plus, la perspective qu’ils apportent à une situation donnée exclue l’avenir et se concentre sur le passé. Lors de l’évaluation de nouveaux exemples, la perspective de l’IA/AA se limite au point de vue contenu dans les données d’apprentissage, d’évaluation et d’essai utilisées pour son perfectionnement. Bien que cette base statique permet à l’IA/AA d’imiter des tâches humaines avec la rapidité et la répétitivité d’un algorithme, elle représente néanmoins une limite considérable. Contrairement à la pensée éthique, l’IA/AA ne peuvent pas considérer un vaste éventail de possibilités futures pendant qu’ils traitent de nouveaux exemples. On décrirait plutôt leur comportement comme l’a écrit Shakespeare, ce qui est passé n’est que prologueNote de bas de page 4.
Alors, qu’en est-il du choc des mondes? Autrement exprimé, que se passe-t-il lorsque l’ambiguïté orientée vers l’avenir de l’équité rencontre l’exactitude du passé, le prologue de l’IA/AA? Il en résulte un nouveau domaine de recherche appelé « équité algorithmique ».
L’assurance de l’équité algorithmique est une préoccupation pressante pour la société d’aujourd’hui. Notre dépendance à l’IA/AA s’accroît et on y trouve de plus en plus de champs d’application. Il devient donc urgent de déterminer si nos utilisations de l’IA/AA respectent notre interprétation d’une société équitable et juste.
En tant que domaine d’étude interdisciplinaire, l’équité algorithmique soulève à la fois des questions philosophiques et des considérations techniques. Par exemple, quelle est la signification de l’équité? Que signifie l’équité dans le contexte de l’IA/AA? Quels liens unissent les différentes définitions de l’équité algorithmique? Comment atteindre l’équité algorithmique? Les notions mathématiques de l’équité présentent-elles des limites?
Dans ce blogue en deux parties, nous explorerons certains aspects clés de l’équité algorithmique dans l’espoir de jeter un nouvel éclairage sur ses possibilités et ses limites. Nous aimerions préciser que le présent document n’est pas un guide pour l’application de l’équité algorithmique d’après les lois fédérales sur la protection des renseignements personnels. L’objectif de cette première partie est d’analyser les principales définitions de l’équité algorithmique afin de contextualiser notre compréhension de cette notion d’un point de vue technique, plutôt que juridique ou politique.
Qu’est-ce que l’équité?
Avant de nous lancer dans une analyse de l’équité algorithmique, il convient de décrire brièvement le concept éthique de l’équité. En tant que type d’équité, l’équité algorithmique partage les propriétés de base de l’équité, les deux étant ainsi du même « genre ». Bien que le lien avec l’IA/AA est ce qui la définit précisément, elle trouve néanmoins ses origines dans le concept éthique de l’équité. Ainsi, une bonne première étape pour comprendre l’équité algorithmique dans son ensemble consiste à explorer la notion de l’équité.
Revenons à Aristote. Ses travaux philosophiques sur l’éthique et la politique cherchaient à découvrir les conditions essentielles dans lesquelles la coexistence humaine doit se dérouler pour atteindre une forme autosuffisante complète. L’équité est l’une de ces conditions.
Aristote fournit plusieurs définitions de l’équité. La plus applicable à notre analyse sur l’équité algorithmique est celle qu’il donne dans son étude des différentes formes de gouvernement. Dans cette étude, Aristote fait la remarque suivante (paraphrase) :
Tout le monde s’entend pour dire que l’équité [ou la « justice »; du mot grec dikaion, qui signifie juste] consiste à traiter les personnes égales avec équité, et les personnes inégales avec iniquité, sans toutefois convenir de la norme qui permet de juger les individus comme étant également (ou inégalement) dignes ou méritantsNote de bas de page 5.
Cette définition contient trois éléments clés sur la nature de l’équité :
- Elle englobe la reconnaissance de similitudes et de différences. L’équité ne sous-entend pas nécessairement l’égalité de traitement entre tous les individus ou groupes. Elle peut aussi intégrer des différences, dans la mesure où celles-ci peuvent être justifiées en tant que dérogations légitimes à la stricte égalité. Donc, les individus ou les groupes peuvent être considérés comme étant semblables ou différents à de multiples égards. L’équité reconnaît et respecte ces deux éléments comme étant essentiels à l’atteinte d’une bonne proportionnalité dans les interactions humaines.
- Elle comprend plusieurs normes. Il n’existe pas d’ensemble unique et universel de critères permettant d’évaluer l’équité d’une situation précise. Plusieurs normes de similitude et de différence existent. Bien entendu, toutes les normes ne sont pas nécessairement appropriées. Certaines peuvent même changer au fil du temps pour tenir compte de l’évolution des idéaux et des valeurs. Pourtant, cette ambiguïté inhérente n’est pas un défaut. Bien au contraire. C’est ce qui confère à l’équité la capacité de « voir » ce qui est juste selon les circonstances en alliant les connaissances du passé aux possibilités futures.
- Les normes sont généralement incompatibles. La similitude et la différence sont des volets fondamentaux de la pensée. Ainsi, il arrive souvent qu’une approche qui satisfait à une norme en matière d’équité entre en conflit avec les critères d’autres approches. Si différentes normes sont applicables et également valables dans certains cas, il est difficile, voire impossible, de toutes les satisfaire. Après tout, déterminer si une norme donnée est appropriée est une question complexe qui combine des considérations juridiques, sociales et éthiques.
Qu’est-ce que l’équité algorithmique?
L’équité algorithmique est un type d’équité principalement soulevé dans le contexte des modèles d’IA/AA utilisés pour le classement. Le classement est un type de tâche de l’IA, tout comme le regroupement, la transcription, la détection des anomalies et la traduction automatique. L’équité algorithmique peut servir à évaluer l’équité de ces tâches d’IA, dans la mesure où leurs résultats peuvent être interprétés comme une forme de classement.
L’IA de type classification est essentiellement un modèle qui étiquette les données selon leur appartenance à différentes catégories. L’étiquette constitue une prédiction, une probabilité d’appartenance. Elle est habituellement dérivée d’une note à valeur réelle que le modèle génère et qui est ensuite comparée à une certaine valeur limite pour déterminer la plage de valeurs numériques de la catégorie. Le classement est donc étroitement lié à la tâche de régression. Les deux tâches sont similaires, sauf que dans le cas de la régression, la prédiction reste sous la forme d’une note à valeur réelle ou d’une probabilité. De nombreuses tâches de classement en IA/AA sont entraînées en tant que tâches de régression auxquelles on ajoute ensuite un seuil pour définir les limites des catégories.
L’équité algorithmique se base sur trois variables présentes dans un classifieur :
- la variable Y, soit la « réalité du terrain », ou la variable cible à prédire;
- la variable R, soit la note ou l’étiquette prédite produite par le modèle;
- la variable A, soit l’attribut sensible qui définit l’appartenance à un groupeNote de bas de page 6.
Les relations entre ces variables déterminent les trois définitions d’équité algorithmique à prendre en considération : la suffisance, la séparation et l’indépendance.
Nous fournirons ci-dessous une brève description de chaque définition, suivie d’une analyse de leurs avantages et de leurs inconvénients. Nous supposerons généralement un classifieur binaire qui associe l’une des étiquettes suivantes aux données : « positive » ou « négative ». Bien que simplifiées, les définitions et les idées dérivées ainsi s’appliquent facilement à des modèles complexes comportant plusieurs catégories.
Suffisance
Il s’agit de la plus ancienne des définitions de l’équité algorithmique. Elle a été proposée par Anne Cleary en 1966 dans son rapport sur le caractère équitable du test d’aptitude scolaire américain (SAT) (en anglais seulement) en tant que prédicteur des résultats des établissements d’enseignement supérieur aux États-Unis.Note de bas de page 7
Officiellement, un modèle d’IA/AA respecte la suffisance lorsque, pour toute note prédite R, la probabilité d’appartenir réellement à la classe positive ou négative (comme indiqué par la réalité du terrain Y) est la même pour tous les groupes A. En notation mathématique, ceci est souvent exprimé par Y ⊥ A | R, ce qui signifie que la réalité du terrain Y est indépendante de l’appartenance au groupe A étant donné une note prédite R.
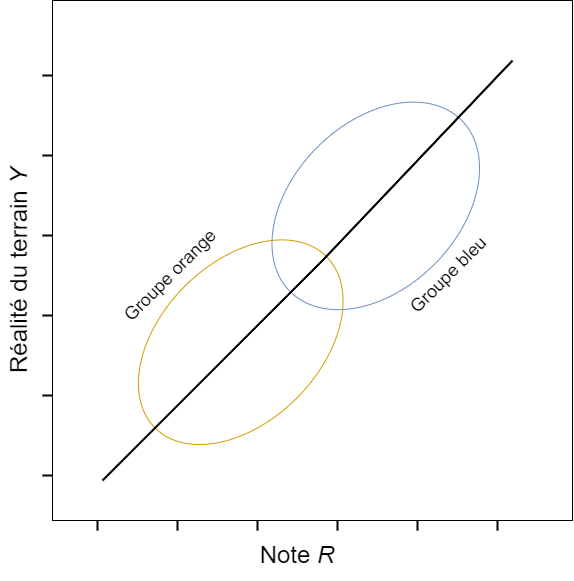
Le fondement intuitif de la suffisance est que R devrait prédire Y; ainsi, un modèle d’IA/AA est équitable si R ne surestime ou ne sous-estime pas systématiquement Y pour les membres d’un groupe quelconque. Autrement dit, les prédictions d’un modèle d’IA/AA équitable devraient être « calibrées de manière égale », de sorte que la distribution des notes R correspond à des valeurs Y semblables, indépendamment de l’appartenance à un groupe. En supposant une distribution normale, la suffisance équivaut à la situation où la droite de régression la mieux ajustée de Y sur R est la même dans tous les groupes : elle aurait la même pente et le même point d’intersection. Ainsi, le modèle assure une parité des valeurs prédictives positives et négatives dans tous les groupes.
Version textuelle de la figure 1
Figure 1 : Exemple d’un modèle de régression de l’IA/AA qui est conforme à la suffisance. L'image représente un diagramme de dispersion X et Y, avec la note R sur l'axe des abscisses X et la réalité du terrain Y sur l'axe des ordonnées Y. Le diagramme représente les données de deux groupes : un groupe orange et un groupe bleu. La courbe de régression commune passe par le milieu des deux diagrammes. Ce modèle calibre donc également les prédictions de la variable cible pour le groupe orange et le groupe bleu.
Version textuelle de la figure 2
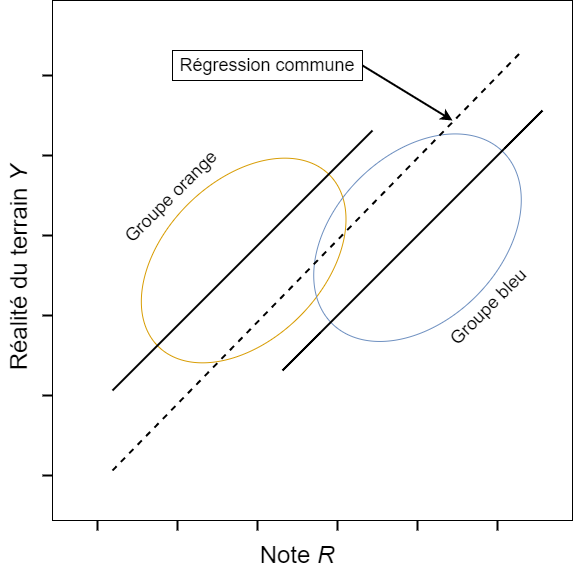
Figure 2 : Exemple d’un modèle de régression de l’IA/AA qui n’est pas conforme à la suffisance. L'image représente un diagramme de dispersion X et Y, avec la note R sur l'axe des abscisses X et la réalité du terrain Y sur l'axe des ordonnées Y. Le diagramme représente les données de deux groupes : un groupe orange et un groupe bleu. La droite de régression commune se trouve en dessous du diagramme de dispersion du groupe orange et au-dessus du diagramme de dispersion du groupe bleu. Ce modèle surestime donc systématiquement la variable cible pour le groupe bleu et sous-estime la variable cible pour le groupe orange.
L’avantage de la suffisance est qu’elle rehausse au maximum la validité prédictive ou l’exactitude globale du modèle d’IA/AA. Les notes R produites par le modèle correspondront à la moyenne la plus élevée des valeurs ou de la fraction Y des cas positifs réels, maximisant ainsi le nombre de prédictions exactes. En d’autres mots, les caractéristiques du modèle d’IA/AA s’adapteront aussi étroitement que possible à la structure sous-jacente des données, compte tenu de la fonction de coût. Ainsi, les organisations qui emploient un modèle d’IA/AA qui satisfait au critère d’équité de suffisance peuvent être assurées que le modèle représente étroitement la structure réelle des données.
Cependant, l’inconvénient de la suffisance est qu’elle permet à un modèle d’IA/AA d’intégrer des formes de discrimination dans ses caractéristiques, tant que la discrimination se traduit par un calibrage égal des valeurs R et Y dans tous les groupes. Par exemple, si un groupe obtient des notes R systématiquement plus faibles (ou plus élevées) qu’un autre, mais que l’adaptation structurelle du modèle d’IA/AA est semblable pour chacun d’entre eux, le modèle d’IA/AA continuera de répondre au critère d’équité de suffisance, même si ses caractéristiques sont fortement corrélées à l’appartenance à un groupe. Cette situation ouvre la porte à d’éventuels abus, si l’appartenance à un groupe est utilisée de manière inappropriée comme variable de substitution pour la variable cible (en anglais seulement) :
Il défie l’entendement de penser qu’une école privée puisse utiliser un « examen » d’admission tellement ancré dans la culture qu’elle admet automatiquement tous les Blancs et rejette automatiquement tous les Noirs, le directeur reconnaissant qu’il y a une faible corrélation entre la race et l’aptitude scolaire, tout en soulignant que l’examen est culturellement équitable selon la définition la plus généralement admise de l’équité culturelle à l’heure actuelleNote de bas de page 8.
Séparation
Officiellement, un modèle d’IA/AA est conforme à la séparation lorsque, pour les cas réels de la classe positive ou négative (comme indiqué par la réalité du terrain Y), la probabilité d’être correctement ou incorrectement classé (en fonction de la note prédite R) est la même dans tous les groupes A. En notation mathématique, ceci est souvent exprimé par R ⊥ A | Y. Ce qui signifie que la note prédite R est indépendante de l’appartenance à un groupe A étant donné une réalité du terrain Y.
Le fondement intuitif de la séparation est que la relation causale entre R et Y peut être inversée. Au lieu que R soit un prédicteur de Y, il est possible de considérer Y comme une capacité qui influe sur R en même temps que sur A. Ainsi, un modèle d’IA/AA n’est équitable que si la probabilité de sélection (ou de rejet) fondée sur R n’est pas corrélée à l’appartenance à un groupe dans un sous-ensemble de personnes ayant le même résultat Y. Autrement dit, un modèle d’IA/AA équitable devrait produire un état de « cotes égalisées », de sorte que l’appartenance à un groupe A n’ait pas d’effet direct sur la note R d’un individu compte tenu de la réalité du terrain Y. Il est alors garanti que tous les groupes connaissent les mêmes taux de faux positifs et de faux négatifs.
Un assouplissement du critère de séparation est possible dans les cas où seul le taux de faux négatifs doit être le même dans tous les groupes, mais pas nécessairement le taux de faux positifs. Si on suppose que l’appartenance à la classe positive est le résultat « favorisé », on parle d’« égalité des chances » (en anglais seulement)Note de bas de page 9.
| Groupe bleu | Groupe orange | |||
|---|---|---|---|---|
| Réel – Positif | Réel – Négatif | Réel – Positif | Réel – Négatif | |
| Prédit – Positif | 45 | 2 | 5 | 18 |
| Prédit – Négatif | 45 | 8 | 5 | 72 |
| Total | 90 | 10 | 10 | 90 |
| Taux d’erreur | Taux de faux négatifs : 45 / 90 = 50 % Taux de faux positifs : 2 / 10 = 20 % |
Taux de faux négatifs : 5 / 10 = 50 % Taux de faux positifs : 18 / 90 = 20 % |
||
| Proportion de positifs | (45 + 2) / 100 = 47 % | (5 + 18) / 100 = 23 % | ||
La séparation a l’avantage de favoriser la priorisation par le modèle d’IA/AA des caractéristiques qui prédisent directement la variable cible, sans s’appuyer indirectement sur l’appartenance à un groupe en tant que variable de substitution de Y. Les notes R produites par le modèle aboutiront à un état de « cotes égalisées », où les individus ayant le même résultat Y bénéficieront de la même probabilité d’être sélectionné (ou rejeté) qu’importe leur appartenance à un groupe. Dans les faits, cela empêche un modèle d’IA/AA d’intégrer d’éventuelles formes de discrimination à ses caractéristiques. Ainsi, les organisations qui emploient un modèle d’IA/AA qui satisfait au critère d’équité de séparation peuvent être assurées que le modèle évite toute influence indue de l’appartenance à un groupe.
Cependant, l’inconvénient de la séparation est qu’elle peut réduire la précision du modèle d’IA/AA dans les cas où l’appartenance à un groupe est réellement corrélée avec la variable cible. Cela se produit lorsque les taux de base d’appartenance à la classe positive ou négative diffèrent entre les groupes. Dans de tels cas, le fait de décourager explicitement le modèle d’IA/AA de détecter et d’apprendre ces corrélations peut conduire à des notes R qui surestiment ou sous-estiment systématiquement la variable cible pour certains groupes. Par exemple, des études ont montré que les taux de récidive des femmes sont considérablement inférieurs à ceux des hommesNote de bas de page 10. Le fait d’ignorer ou de supprimer cette corrélation peut conduire à un modèle d’IA/AA qui surestime la probabilité de récidive des femmes (en anglais seulement)Note de bas de page 11.
Indépendance
Officiellement, un modèle d’IA/AA respecte l’indépendance lorsque, indépendamment des cas réels de la classe positive ou négative (comme indiqué par la réalité du terrain Y), la probabilité d’être attribué à la classe positive (sur la base de la note prédite R) est la même dans tous les groupes A. En notation mathématique, ceci est souvent exprimé par R ⊥ A, ce qui signifie que la note prédite R est indépendante de l’appartenance au groupe A, quelle que soit la réalité du terrain Y.
Le fondement intuitif de l’indépendance est la conviction qu’en définitive les données démographiques de la population dans son ensemble devraient servir de réalité du terrain pour un modèle d’IA/AA, c’est-à-dire que les prédictions d’un modèle d’IA/AA devraient être « indépendantes » de la réalité du terrain. Ainsi, un modèle d’IA/AA n’est équitable que s’il attribue la même proportion de membres de chaque groupe démographique à la classe positive ou négative, quelle que soit la proportion réelle de cas dans chaque classe. Autrement dit, même s’il existe des différences dans les taux de base entre les groupes, le modèle d’IA/AA doit agir comme s’il n’existait aucune corrélation entre l’appartenance à un groupe et la variable cible. Cela équivaut à la notion de « parité statistique ».
| Groupe bleu | Groupe orange | |||
|---|---|---|---|---|
| Réel – Positif | Réel – Négatif | Réel – Positif | Réel – Négatif | |
| Prédit – Positif | 31 | 1 | 8 | 24 |
| Prédit – Négatif | 59 | 9 | 2 | 66 |
| Total | 90 | 10 | 10 | 90 |
| Taux d’erreur | Taux de faux négatifs : 59 / 90 = 66 % Taux de faux positifs : 1 / 10 = 10 % |
Taux de faux négatifs : 2 / 10 = 20 % Taux de faux positifs : 24 / 90 = 27 % |
||
| Proportion positive | (31 + 1) / 100 = 32 % | (8 + 24) / 100 = 32 % | ||
L’avantage de l’indépendance tient à sa simplicité. Si la variable cible n’est pas corrélée avec l’appartenance à un groupe, la proportion de notes prédites par le modèle d’IA/AA ne devrait pas l’être non plus. Dans les faits, l’indépendance suppose que la variable cible est un attribut universel partagé par tous. Ainsi, les organisations qui emploient un modèle d’IA/AA qui satisfait au critère d’équité d’indépendance peuvent être assurées que le modèle assure l’égalisation des résultats entre les groupes.
Cependant, l’indépendance comporte un inconvénient : elle introduit une forme de discrimination contre des individus (en anglais seulement) dans les cas où les taux de base diffèrent d’un groupe à l’autreNote de bas de page 12. Le modèle d’IA/AA sélectionnera à tort une proportion plus faible de cas positifs réels dans les groupes ayant des taux de base plus élevés et une proportion plus élevée de cas négatifs réels dans les groupes ayant des taux de base plus faibles. Dans les faits, on constate une augmentation des faux négatifs pour les groupes ayant des taux de base plus élevés et une augmentation des faux positifs pour les groupes ayant des taux de base plus faibles. Par exemple, dans le Tableau 2, la proportion globale de prédictions positives est la même (32 %) dans les groupes bleu et orange, ce qui respecte l’indépendance. Cependant, le taux de base des individus de la classe positive diffère. Pour le groupe bleu, il est de 90 % (90/100), alors qu’il est de 10 % (10/100) pour le groupe orange. Par conséquent, 66 % (59/90) des personnes qualifiées du groupe bleu sont attribuées à tort à la classe négative, contre 20 % (2/10) dans le groupe orange.
Quel est le lien entre les définitions?
À la lumière de ce qui précède, il paraît évident que les trois principales définitions de l’équité algorithmique sont incompatibles entre elles. Même si chacune de ces définitions fournit un cadre d’équité pour les classifieurs, elles ne peuvent être simultanément respectées, sauf dans des cas particuliers, en présence de circonstances contraignantes et au moyen de solutions évidentes.
Il existe des preuves formelles pour démontrer cette évidenceNote de bas de page 13 (en anglais seulement). Or, d’un point de vue conceptuel, l’incompatibilité en va de ce qui suit :
- La suffisance procure un maximum d’exactitude en évitant de réduire au minimum les différences entre les groupes;
- La séparation réduit au minimum les différences entre les groupes en évitant de fournir un maximum d’exactitude;
- L’indépendance suppose qu’il n’y a aucune différence entre les groupes, peu importe l’exactitude.
Dans la pratique, cette relation entre les définitions revient à un compromis entre un maximum d’exactitude et un minimum de différences entre les groupes. De manière générale, plus une définition de l’équité algorithmique accroît l’exactitude du modèle d’IA/AA, moins elle peut réduire au minimum les effets des différents taux de base entre les groupes, et vice versa.
Cette incompatibilité tient au fait que chaque définition intègre une interprétation différente de la similitude et de la différence par rapport aux individus. La suffisance ne considère la similitude que du point de vue de la validité prédictive du modèle d’IA/AA, tandis que l’indépendance aborde la similitude uniquement du point de vue du taux de base entre les groupes. Aussi, la suffisance permet de tenir compte des différences entre les groupes, alors que l’indépendance ne le permet pas. La perspective de la séparation se situe quelque part au milieu.
Malgré leur incompatibilité générale, l’ensemble ou une partie des définitions pourrait être simultanément respectée. Cependant, l’espace de solution qui permet la compatibilité se situe aux marges du compromis entre un maximum d’exactitude et un minimum de différences entre les groupes. C’est pourquoi les conditions sont difficiles à obtenir en pratique. Même lorsqu’elles sont présentes, la solution peut ne présenter qu’une compatibilité partielle ou superficielle avec d’autres définitions. Voici les deux situations à prendre en compte :
- Une prédiction parfaite. Si l’espace des attributs de la classe positive et de la classe négative est clairement divisé (sans chevauchement), il est possible de respecter la suffisance et la séparation en élaborant un classifieur qui apprend à attribuer avec certitude chaque individu à la bonne classe selon ses caractéristiques respectives. En effet, cela donnerait un modèle avec des valeurs prédictives de 1 et des taux d’erreur de 0 dans tous les groupes.
- Des taux de base égaux. Si la proportion de membres de la classe positive est la même dans tous les groupes, il est alors possible de respecter les trois définitions en attribuant simplement à chaque individu de la classe positive une note égale au taux de base. Bien que superficiel par nature, un tel classifieur garantirait néanmoins l’égalité pour ce qui est des valeurs prédictives, du taux d’erreur et de la proportionnalité des membres de la classe positive et négative dans tous les groupes. Une solution plus précise et rigoureuse pourrait être possible, mais elle n’est pas garantieNote de bas de page 14 (en anglais seulement).
Conclusion
Dans ce premier volet de notre série de blogues sur l’équité algorithmique, nous avons acquis certaines connaissances sur l’histoire, le contexte et la nature de l’équité algorithmique, ainsi que les défis s’y rattachant.
- L’équité algorithmique est un domaine de recherche nouveau qui apparaît au point de rencontre entre l’ambiguïté de l’équité – orientée vers le futur – et l’exactitude [appuyée de] – ce qui est passé n’est que prologue – de l’IA/AA.
- En tant que type d’équité, l’équité algorithmique partage les propriétés de base du concept éthique d’équité :
- elle suppose la reconnaissance de similitudes et de différences;
- elle repose sur de multiples normes;
- ces normes sont généralement incompatibles.
- De manière générale, il existe trois définitions principales de l’équité algorithmique :
- la suffisance ou la parité des valeurs prédictives;
- la séparation ou la parité des taux d’erreurs;
- l’indépendance ou la parité statistique.
- Les définitions sont habituellement incompatibles entre elles en raison du compromis inhérent entre l’optimisation de l’exactitude et la réduction au minimum des différences entre les groupes.
- Il est possible que toutes les définitions, voire seulement certaines d’entre elles, soient simultanément respectées. Or, cela se produit dans des cas particuliers, en présence de circonstances contraignantes, et au moyen de solutions évidentes.
Les éléments présentés dans cette première partie nous révèlent la complexité de l’équité algorithmique. D’une part, elle propose des définitions mathématiques utiles qui fournissent un cadre pour évaluer comment nos utilisations de l’IA/AA peuvent être rendues plus compatibles avec l’idée d’une société équitable et juste. Pourtant, l’incompatibilité générale entre les définitions pose aussi des problèmes importants aux praticiens. Plusieurs questions subsistent : notamment, quelles mesures peuvent être appliquées pour contribuer à l’équité algorithmique? Comment choisir parmi les définitions? Quelles sont les limites des notions mathématiques de l’équité?
Veuillez passer au deuxième volet de notre série de blogues sur l’équité algorithmique, où nous aborderons ces questions et d’autres encore.

